Simple proof of solution to the Monty Hall problem

The Monty Hall problem was first famously solved by Marilyn vos Savant in 1990, and infamously argued by many intellects. The premise is roughly as follows:

There are three doors: behind two are goats, and behind one is a car. You will receive the object behind the one you open. You must first choose one door, and the host (who knows the contents of all three doors) will then open one of the two remaining doors and show you a goat. You can then choose to open your original choice, or switch your choice to the remaining door. Are you more likely to get the car if you switch?

Here is a visual walk-through of the solution by a simple decision tree.

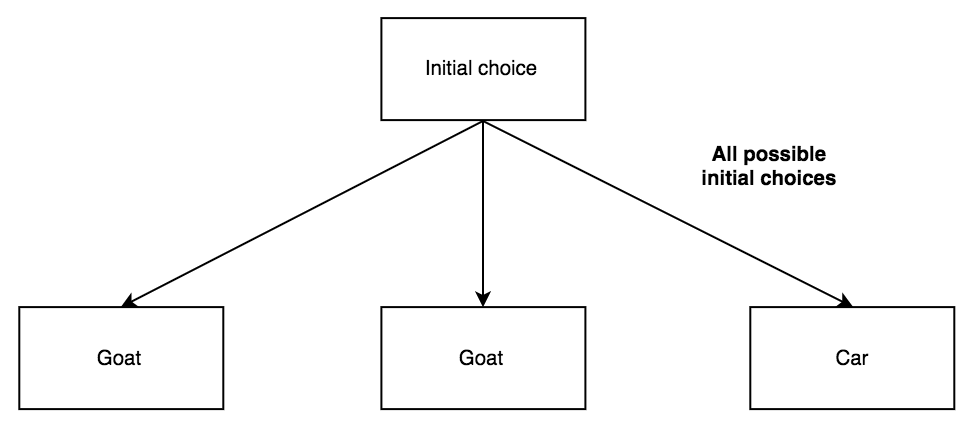
There are three doors, so our initial choice is as follows:

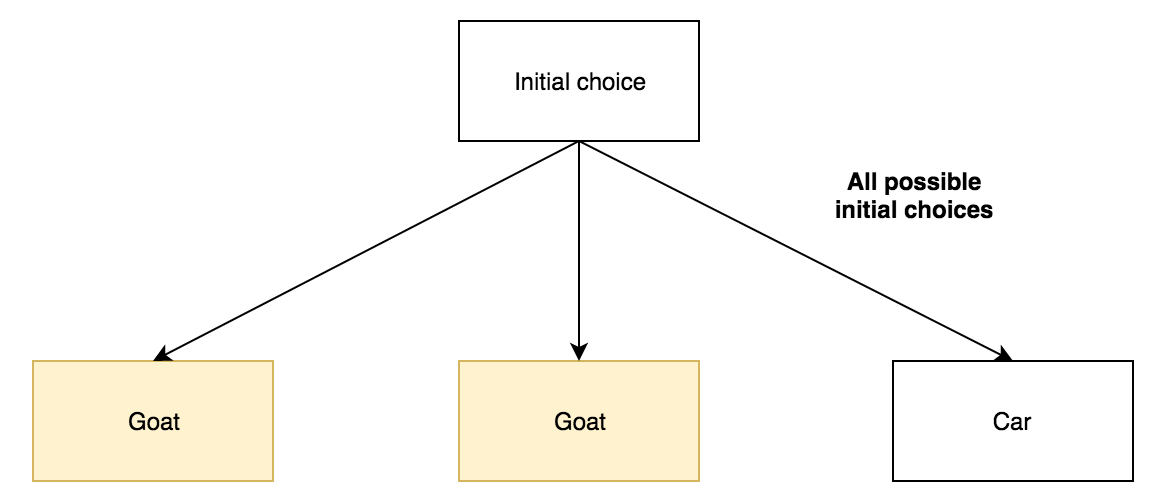
Once you have chosen a door, the host must open one of the two remaining doors and show you a goat. Regardless of whether your first choice was the goat or the car, the host must show you one of the goat doors, highlighted in yellow.

Now we have two possible outcomes. If the initial choice was a goat, then the host showed you the other goat door, and so the remaining unknown door must be the car. If the initial choice was the car, then changing our choice would definitely result in a goat.

The outcome for each of the initial choices if we switch our choice is highlighted in green below.

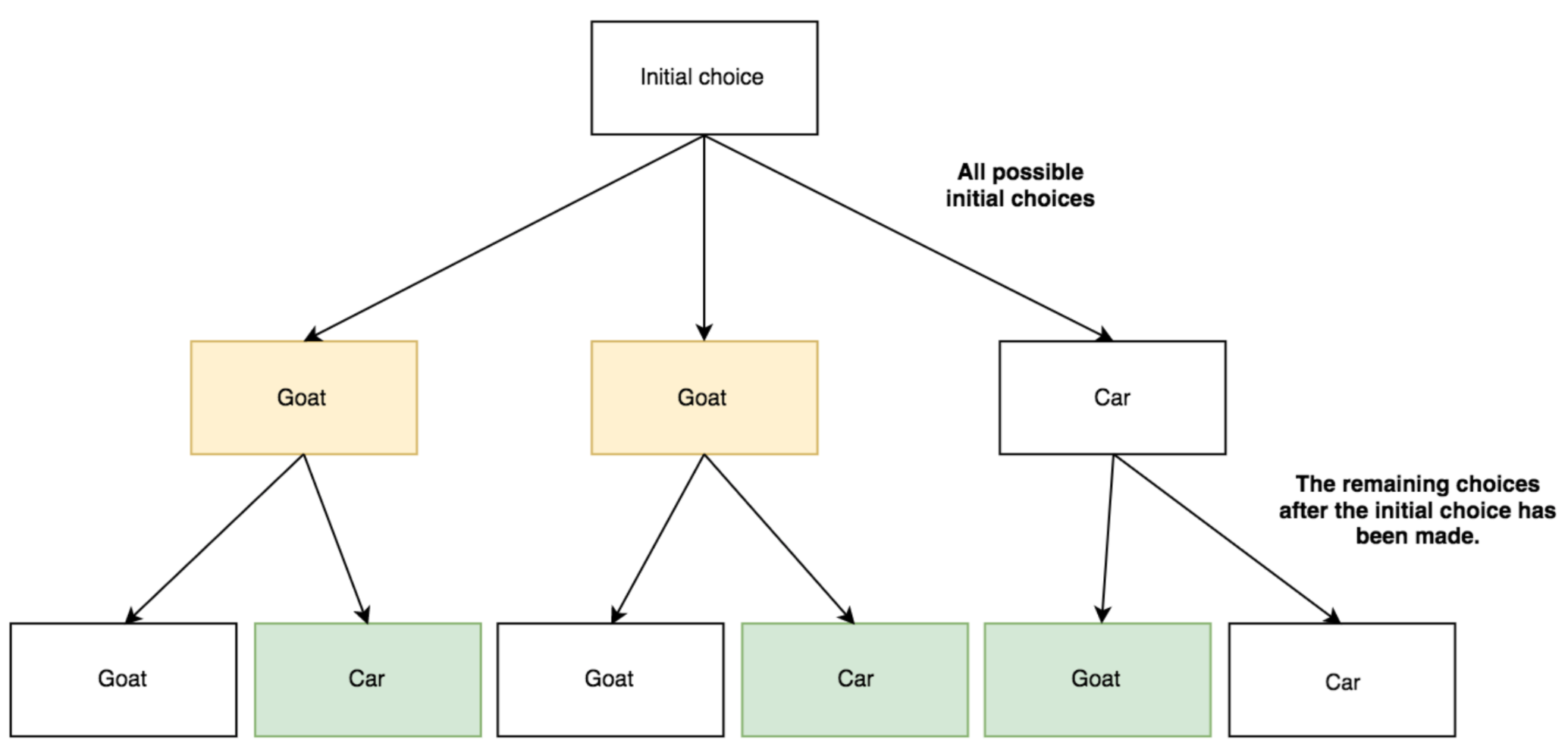
It is now clear that the likelihood of getting a car if we switch from our intitial choice is 2/3! So the answer is yes. We should always switch our choice. You are more likely to get a car if you switch your choice to the remaining door.